Introduction:
Welcome to Episode 12 of our Unsupervised Learning series! We're thrilled to have you join us on this journey as we unravel the mysteries of clustering algorithms in the fascinating world of machine learning.
Clustering is a fantastic tool that helps algorithms discern patterns without needing explicit guidance. In this episode, we'll explore its essence and its contrast with supervised learning, as well as the many ways it's used in real-world applications, from grouping news articles to analyzing DNA data.
We'll demystify the fundamental concepts of clustering algorithms and show you how they have significant real-world implications. By the end of this episode, you'll have a deeper understanding of clustering algorithms and their potential.
In our next installment, we'll take an in-depth look at the widely used k-means algorithm. Join us on this exhilarating journey through the landscapes of unsupervised learning, as we uncover the power and potential of clustering algorithms in deciphering the complexities of uncharted data.
Unsupervised Learning Landscape
Overview of Unsupervised Learning Algorithms
Unsupervised learning algorithms operate without the crutch of labeled data, making them well-suited for scenarios where the inherent structure of the data is elusive or undefined. This landscape encompasses a diverse array of algorithms, each designed to unravel distinct facets of hidden patterns. From clustering and dimensionality reduction to association and anomaly detection, the unsupervised learning toolbox is rich with methods that illuminate the latent features embedded within datasets.
Absence of Target Labels in Unsupervised Learning
A defining characteristic of unsupervised learning is the absence of target labels. Unlike supervised learning, where algorithms are guided by predefined outcomes, unsupervised learning algorithms explore datasets devoid of explicit labels or categories. This characteristic sets the stage for a unique exploration, where the algorithm's task is not to predict a predetermined "answer" but to uncover the inherent structure and relationships within the data.
Clustering Algorithms
In the heart of unsupervised learning lies the captivating world of clustering algorithms. These algorithms, designed to discern patterns and group similar data points together, serve as the compass guiding us through the uncharted territories of unlabeled datasets. Let's embark on a journey to demystify the core concepts and applications of clustering algorithms.
Introduction to Clustering Algorithms
Clustering algorithms are unsupervised learning techniques that examine datasets to identify inherent structures and relationships among data points. The primary goal is to group together elements that share similarities, unveiling clusters or segments within the data. Unlike supervised learning, where explicit labels guide the learning process, clustering algorithms operate independently, allowing patterns to emerge organically.
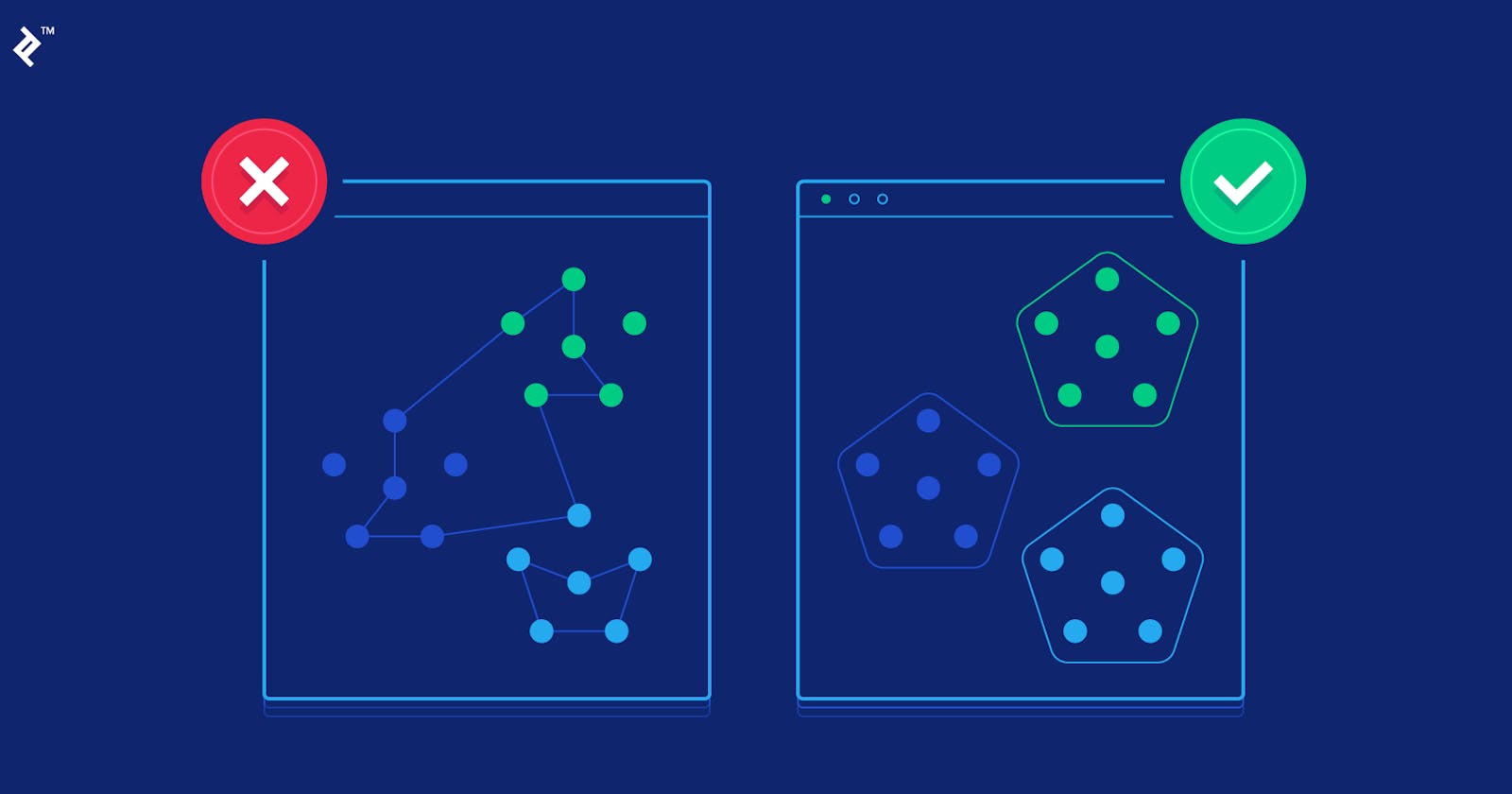
Focus on Identifying Clusters in Data
The essence of clustering lies in its ability to identify clusters—groups of data points that exhibit similarities based on certain features. Imagine a dataset spread across a two-dimensional space; a clustering algorithm would autonomously categorize these points into meaningful groups without prior knowledge of what those groups might represent. This intrinsic ability makes clustering algorithms versatile tools for exploring datasets where the underlying structure is not apparent.
Applications of Clustering
In the dynamic landscape of machine learning, clustering algorithms find themselves at the forefront, offering invaluable insights and practical solutions across diverse domains. From shaping marketing strategies to unraveling the mysteries of genetic data and delving into the cosmos, the applications of clustering algorithms are as varied as they are impactful. Let's explore how clustering algorithms manifest in real-world scenarios.
News Article Grouping
In the fast-paced world of journalism, clustering algorithms prove instrumental in grouping similar news articles together. By identifying patterns and shared themes within an expansive collection of articles, clustering facilitates efficient content organization and enhances the user experience for readers seeking related information.
Market Segmentation in Education
At the intersection of education and technology, clustering algorithms contribute to market segmentation. In the case of deeplearning.ai, understanding the diverse motivations of learners—whether driven by skill development, career advancement, or staying abreast of AI trends—allows for tailored educational offerings. Clustering aids in recognizing these distinct learner clusters and tailoring educational content to meet specific needs.
DNA Data Analysis
Clustering algorithms play a pivotal role in the field of genetics by analyzing DNA data. When confronted with genetic expression data from different individuals, clustering helps group them based on shared traits. This application is instrumental in understanding genetic patterns, identifying commonalities, and potentially unlocking insights into hereditary traits and diseases.
Clustering in Astronomical Data Analysis
Venturing beyond our planet, astronomers harness clustering algorithms for the analysis of astronomical data. As celestial bodies populate the vastness of space, clustering aids in grouping these entities together. This enables astronomers to discern coherent structures, such as galaxies, and conduct detailed analyses to deepen our understanding of the cosmos.
Versatility Across Various Domains
The versatility of clustering algorithms extends beyond these specific applications. From customer segmentation in business to anomaly detection in cybersecurity, clustering proves to be a versatile tool for revealing hidden patterns, guiding decision-making processes, and extracting valuable insights from complex datasets.
K-mean Algorithm Intuition

Let's take a closer look at the K-means clustering algorithm and how it works. To better understand it, let me walk you through an example. I have plotted a data set with 30 unlabeled training examples, meaning there are 30 points. Our goal is to run K-means on this data set.
In the K-means algorithm, the first step is to randomly select the centers of the clusters that need to be found. This is essentially a guess of where the clusters might be located. For instance, if you want to find two clusters, you need to randomly pick two points as the centers of these clusters. These initial guesses may not be accurate, but they help to start the process.
One important thing to remember is that K-means repeatedly does two things: it assigns points to cluster centroids and moves cluster centroids. The first step involves going through each point and determining whether it is closer to the red or blue cross. The centers of the clusters are called cluster centroids, and they are initially chosen randomly.
After assigning each point to its closest cluster centroid, the algorithm then moves the centroids to the average position of the points in the cluster. This process is then repeated until the centroids no longer move or until a maximum number of iterations is reached.
It's important to note that K-means is an iterative process and the initial guesses for the cluster centroids may not be accurate. However, by repeatedly assigning points to the closest centroid and moving the centroids, K-means can accurately identify clusters in data.
The first step of the algorithm is to assign each point to a cluster centroid. We do this by painting the points red or blue, depending on which centroid they are closer to. The red and blue centroids represent the two clusters.
The second step is to calculate the average of all the points in each cluster and move the centroid to that location. This process is repeated until the centroids no longer move significantly.
Once we have the new centroid locations, we look at each point again and assign it to the closer centroid. This changes the color of some points from red to blue or vice versa.
Then, we repeat the second part of the K-means algorithm, which involves computing the average location of all the red dots and the average location of all the blue dots. This results in moving the Red Cross and the Blue Cross to new locations. We repeat this process by coloring the points red or blue, depending on which cluster centroid is closer to them. We then take the average location of all the red dots and the average location of all the blue dots, move the cluster centroids to these new locations, and repeat the process. We keep doing this until there are no further changes in the point colors or the locations of the cluster centroids. This means that the K-means algorithm has converged. In this example, K-means has successfully identified two clusters: one with points at the top and one with points at the bottom. The two key steps in K-means are assigning every point to its nearest cluster centroid and moving each cluster centroid to the mean of all the points assigned to it.
In the next section, we will formalize this process and write out the algorithm.
The mathematics behind the K-means algorithm

The K-means algorithm can be broken down into several steps. First, you need to randomly initialize K cluster centroids, which are denoted as Mu 1, Mu 2, through Mu k. Let's say you have two cluster centroids to find, which we represent as the red cross and the blue cross. In this example, K equals two. The red cross represents cluster centroid one, and the blue cross represents cluster centroid two. These centroids are vectors that have the same dimension as your training examples, X1 through X30. In our example, all the training examples have two features, so Mu 1 and Mu 2 are also two-dimensional vectors.
After randomly initializing the K cluster centroids, K-means then repeatedly carry out two steps. The first step is to assign points to the cluster centroids, which involves giving each point a color, either red or blue, corresponding to assigning them to cluster centroids one or two when K is equal to two. For each training example, you will set c^i to be equal to the index, which can be anything from one to K, of the cluster centroid closest to the training example x^i. Mathematically, this can be written as computing the distance between x^i and Mu k. You want to find the value of k that minimizes this distance because it corresponds to the cluster centroid Mu k that is closest to the training example x^i.
In practice, it's more convenient to minimize the squared distance because the cluster centroid with the smallest square distance should be the same as the cluster centroid with the smallest distance. When you implement this algorithm, you will find that it's a little bit more convenient to minimize the squared distance. This week's optional labs and practice labs show you how to implement this in code for yourself.
As a concrete example, consider the two points in the image. The point at the top is closer to the red cluster centroid (Mu 1), so if it were a training example x^1, we would set c^1 to be equal to 1. The point on the right is closer to the blue cluster centroid (Mu 2), so if it were the 12th training example, we would set the corresponding cluster assignment variable to two. That's the first step of the K-means algorithm: assigning points to cluster centroids.

In the second step of K-means clustering, we need to move the cluster centroids. This means that for each cluster k, ranging from 1 to K, we will update the cluster centroid location to be the average or mean of the points assigned to that cluster.
To do this, we'll take all the points that belong to a particular cluster, say the red points, and average out their positions on the horizontal axis and the vertical axis. The resulting mean is the new location of the cluster centroid for the red cluster. Similarly, we'll repeat this process for all other clusters as well.
To compute the average value of a cluster's points, we'll add up the values of each feature (x1, x2, etc.) for all the points in the cluster and divide the sum by the total number of points in the cluster. This will give us the new location of the cluster centroid for that particular cluster.
It's important to note that each point in a cluster has n features, and so the new location of the cluster centroid will also have n features.
Optimization Algorithm

In the earlier episodes of this specialization, you were introduced to many supervised learning algorithms that take a training set and optimize a cost function using gradient descent or other similar algorithms. In the last section, you saw the K-means algorithm, which also optimizes a specific cost function. Although it uses a different optimization algorithm than gradient descent, it is still optimizing the cost function. Let's take a closer look at what this means.
To start, let's refresh our memory on the notation we've been using. The index of the cluster to which training example XI is currently assigned is denoted by CI, and new K is the location of cluster centroid k. When lowercase K equals CI, mu subscript CI is the cluster centroid of the cluster to which example XI has been assigned. For example, if I look at the 10th training example and ask what's the location of the clustering centroids to which it has been assigned, I would look up C10. This will give me a number from one to K that tells me which centroid it was assigned to, and then mu subscript C-10 is the location of the cluster centroid to which the example has been assigned.
With this notation, the cost function that K-means minimizes can be written as J, which is a function of C1 through CM (the assignments of points to clusters) and mu subscript K (the locations of all the cluster centroids). The expression on the right side of the equation is the average squared distance between every training example XI and its assigned cluster centroid mu subscript CI. In other words, J is the average squared distance between every training example and the location of the cluster centroid to which it has been assigned.
The K-means algorithm tries to find assignments of points to clusters and locations of cluster centroids that minimize the squared distance between the training examples and their assigned centroids.

In the earlier section, you saw what happens partway into the run of K means. To compute the cost function, you would measure the distance between every blue point and compute the square, then do the same for every red point. The average of the squares of all these differences for the red and blue points is the value of the cost function J at this particular configuration of the parameters for K-means. On every step, they try to update the cluster assignments C1 through C30 or update the positions of the cluster centralism, U1 and U2, to keep reducing this cost function J. This cost function J is also called the distortion function in the literature, though this may not be the best name. If you hear someone talk about the K-means algorithm and the distortion or the distortion cost function, they are referring to what this formula J is computing.

Let's take a closer look at the K-means algorithm and why it seeks to minimize the cost function J. During the first step of K-means, where points are assigned to cluster centroids, the algorithm tries to update C1 through CM to minimize the cost function J while holding mu one through mu K constant. In contrast, during the second step where the centroid is moved, the algorithm tries to update new one through mu K to minimize the cost function or the distortion as much as possible while holding C1 through CM constant.
To minimize the distance or the square distance between a training example XI and the location of the centroid it is assigned to, the algorithm assigns XI to the closest cluster centroid. For example, if there are two cluster centroids and a single training example XI, the square distance between XI and centroid one would be larger than the square distance between XI and centroid two. Therefore, the algorithm assigns XI to the closer centroid to minimize this term.
The second step involves choosing mu K to be the average and mean of the points assigned to the centroid, which is the choice of terms mu that will minimize the expression.
Overall, the K-means algorithm assigns points to the closest centroid to minimize the distance or square distance and updates the centroids to minimize the cost function or distortion as much as possible.

In the K-means algorithm, the cost function J is optimized. This cost function measures the sum of the squared distances between each point in a cluster and its centroid. The goal is to minimize this cost function by adjusting the position of the centroids.
To determine if the algorithm has converged, there are two things to consider. First, the cost function should go down or stay the same on every iteration. If it ever goes up, there is a bug in the code. Second, once the cost function stops decreasing, it means that the algorithm has converged.
It is also possible to take advantage of the cost function by using multiple random initializations of the centroid. By doing this, it is possible to find better clusters that minimize the cost function.
Initializing K-means Algorithm
To start the K-means clustering algorithm, the first step is to choose random locations as initial guesses for the cluster centroids mu one through mu K. But how do you actually take that random guess? In this section, we will take a look at how you can implement this first step, as well as how you can take multiple attempts at the initial guesses with mu one through mu K, resulting in finding a better set of clusters.
When running K-means, it is recommended that the number of cluster centroids K be less than or equal to the number of training examples m. It doesn't make sense to have K greater than m as there won't be enough training examples to have at least one training example per cluster centroid. In our earlier example, we had K equals two and m equals 30.
The most common way to choose the cluster centroids is to randomly pick K training examples. For instance, if you randomly pick two training examples from a training set, you might end up picking one and another. Then, you would set mu one through mu K equal to these K training examples. You might initialize your red cluster centroid here and your blue cluster centroid over there, in the example where K was equal to two. If this was your random initialization, you might end up with K-means deciding that these are the two classes in the data set.
It is worth noting that this method of initializing the cluster centroids is a little different from what was used in the illustration in the earlier videos, where the cluster centroids mu one and mu two were initialized to just random points, rather than sitting on top of specific training examples. This was done to make the illustrations clearer. However, what is being shown in this slide is actually a much more commonly used way of initializing the cluster centroids.
With this method, there is a chance that you end up with an initialization of the cluster centroids where the red cross is here and maybe the blue cross is there. Depending on how you choose the random initial central centroids, K-means will end up picking a different set of clusters for your data set.

In this example, we will analyze a data set and attempt to identify three clusters, with k equaling to three. If you run K-means with one random initialization of the cluster centroid, you might get a good clustering of the data into three distinct clusters. However, with a different initialization, you may get a suboptimal result, such as a local minimum. To avoid this issue, you can run K-means multiple times with different initializations. Once you have several distinct clusterings, you can calculate the cost function J for each of them and select the one with the smallest value. This will ensure that you end up with the best clustering possible.

Here is the Algorithm, To use 100 random initializations for K-means, you need to run K-means 100 times with random initialization using the method explained in the video. First, pick K training examples, and let the cluster centroids be the locations of those K training examples. Use this random initialization to run the K-means algorithm to convergence, which will provide you with a set of cluster assignments and centroids. Finally, compute the distortion function as the cost function.
After repeating this process 100 times, pick the set of clusters that gave the lowest cost. This technique often results in a much better set of clusters with a lower distortion function than running K-means only once. Using between 50 to 1000 random initializations is common. However, running it more than 1000 times can become computationally expensive and may result in diminishing returns. Trying at least 50 or 100 random initializations is often better than having only one shot at picking a good random initialization.
Using this technique, you are much more likely to end up with a good choice of clusters on top and less superior local minima down at the bottom. Hence, using more than one random initialization is recommended when using the K-means algorithm as it helps minimize the distortion cost function and find a better choice for the cluster centroids.
Choosing the number of clusters

The k-means algorithm requires the number of clusters you want it to find as one of its inputs, which is denoted as k. However, deciding the appropriate number of clusters to be used can be challenging. For instance, you may want to use two, three, five, or ten clusters, but how do you decide which one to use?
In most clustering problems, determining the right value of K is quite ambiguous. If I were to show the same data set to different people and ask them how many clusters they see, there would be varying responses. Some would see two distinct clusters, while others would see four distinct clusters.
This is because clustering is an unsupervised learning algorithm, and you're not given specific labels to try and replicate. In many cases, the data itself doesn't provide a clear indicator of how many clusters there are. Therefore, it's truly ambiguous whether this data has two, three, or four clusters.
For instance, if you consider the red cluster and the two blue clusters, it's unclear whether they should be considered as one cluster or two separate clusters.

One common problem when using K-means is deciding how many clusters to use for a given application. There are several techniques in the academic literature to automatically choose the number of clusters. One such technique is the elbow method. This method involves running K-means with a range of values for K, and then plotting the cost function or the distortion function J as a function of the number of clusters. When few clusters are used, the cost function will be high. However, as the number of clusters increases, the cost function will decrease. The elbow method looks for the point at which the cost function decreases more slowly after a certain number of clusters, which is called the elbow. In practice, this method can provide insight into choosing the right number of clusters. However, it is not always reliable because the optimal number of clusters is often ambiguous. Choosing K to minimize the cost function J is not a good technique because it often leads to selecting the largest possible value of K, which is not always the best choice.
When you use K-means, it is often to create clusters that you can use for some later purpose. This means that you will take the clusters and use them for something else. To evaluate K-means, it is recommended that you assess how well it performs for that later purpose.
To illustrate this, let's take the example of t-shirt sizing. You can run K-means on a dataset to find the clusters that will help you size your small, medium, and large t-shirts. However, how many t-shirt sizes should there be? It's ambiguous. If you run K-means with five clusters, you might get clusters that size t-shirts according to extra small, small, medium, large, and extra large. Both of these groupings are valid, but you need to decide which one makes more sense for your t-shirt business.
To make this decision, you can run K-means with K equals 3 and K equals 5. Then, compare the two solutions and decide based on the trade-off between how well the t-shirts fit and how much it will cost to manufacture and ship five types of t-shirts instead of three.
In the programming exercise, you will see an application of K-means to image compression. There will be a trade-off between the quality of the compressed image and how much you can compress the image to save space. You can use this trade-off to decide the best value of K based on how good you want the image to look versus how large you want the compressed image size to be.
That's all for the K-means clustering algorithm.
Lab Work for K-means Algorithm: K-means Practical Notebook link
🎙️ Message for Next Episode:
In this episode, we will learn the theory behind clustering algorithms, specifically the k-means algorithm. In the upcoming episode, we will apply this theoretical knowledge to a practical scenario and learn how to implement this knowledge in the real world.
Resources For Further Research
Coursera - Machine Learning Specialization
This Article is heavily inspired by this Course so I will also recommend you to check this course out, there is an option to watch the
course for freeor you can buy the course to gain aSpecialization Certificate.Optional labs provided in this article are from this course itself.
"Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow" by Aurélien Géron:
- A practical guide covering various machine learning concepts and implementations.
By the way…
Call to action
Hi, Everydaycodings— I’m building a newsletter that covers deep topics in the space of engineering. If that sounds interesting, subscribe and don’t miss anything. If you have some thoughts you’d like to share or a topic suggestion, reach out to me via LinkedIn or X(Twitter).
References
And if you’re interested in diving deeper into these concepts, here are some great starting points:
Kaggle Stories - Each episode of Kaggle Stories takes you on a journey behind the scenes of a Kaggle notebook project, breaking down tech stuff into simple stories.
Machine Learning - This series covers ML fundamentals & techniques to apply ML to solve real-world problems using Python & real datasets while highlighting best practices & limits.